Joshua Maglione
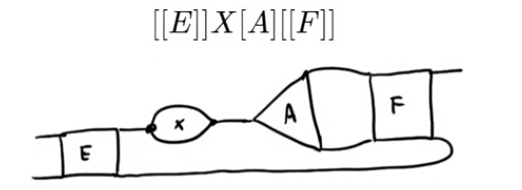
Abstract By bringing in tools from multilinear algebra, we introduce a general method to aid in the computation of isomorphism for groups. Of particular interest are nilpotent groups where the only classically known proper nontrivial characteristic subgroup is the derived subgroup. This family of groups poses the biggest challenge to all modern approaches. Through structural analysis of the biadditive commutator map, we leverage the representation theory of Lie algebras to prove efficiency for families of nilpotent groups. We report on joint work with Peter A. Brooksbank, Uriya First, and James B. Wilson.
Speaker: Josh Maglione, U. Bielefeld
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
Additional Questions?
If you have additional questions, feel free to reach out to a maintainer / contributor on the contact page.
