The Tame Genus package provides polynomial-time algorithms to compute automorphism groups and decide isomorphism for “tame genus” $p$-groups and alternating $3$-tensors. These include
- $d$-generator $p$-groups of order $p^{d + 2}$, exponent $p$, and class $2$,
- $3$-tensors of the form $\mathbb{F}_q^d\times \mathbb{F}_q^d\rightarrowtail \mathbb{F}_q^2$.
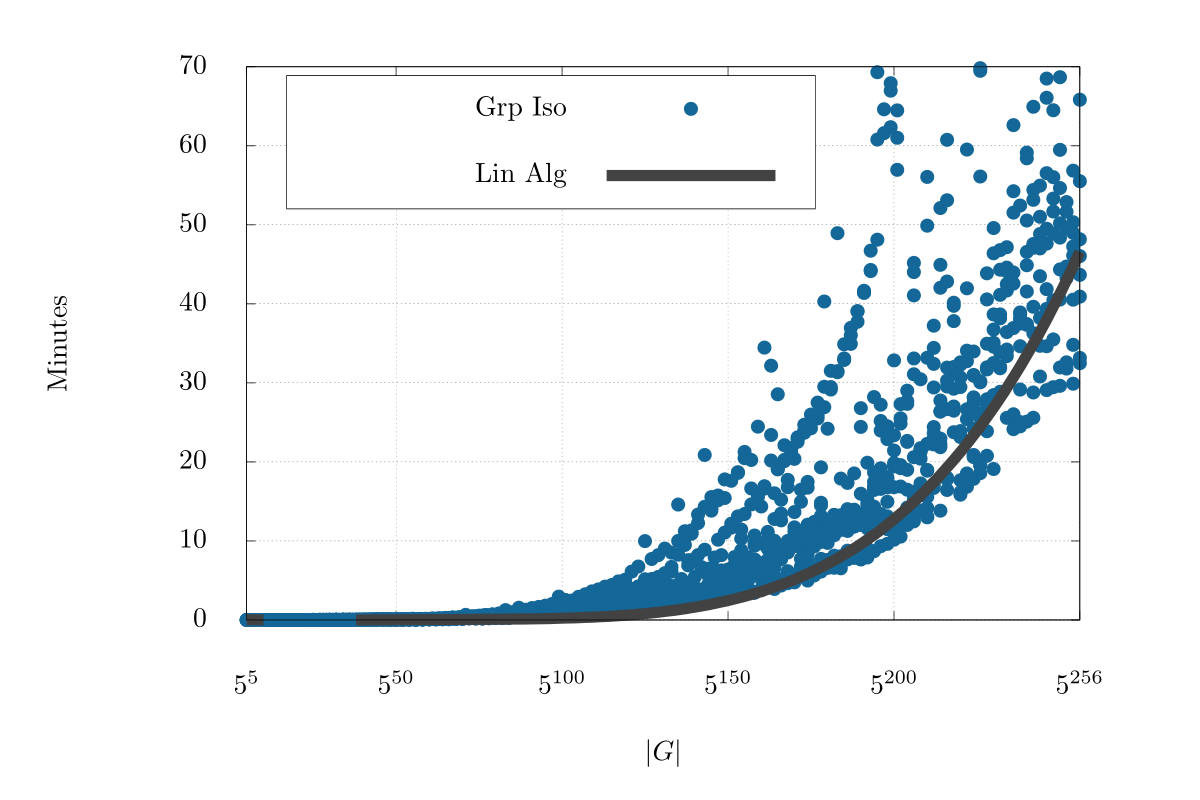
These algorithms can decide isomorphism on tame genus groups of of order $5^{256}$ in less than an hour. They are based on work done by P. A. Brooksbank, J. Maglione, and J. B. Wilson (J. Algebra 2017). Sample runtimes for deciding isomorphism can be found in the same paper.
How to get started
To see if a $p$-group or $3$-tensor is suitable for the Tame Genus package, use either
IsTameGenusGroup, orIsTameGenusTensor.
To build examples of your own, can use
TGRandomGroup, andRandomGenus2Group.
Decide isomorphism, construct the automorphism group, or determine a canonical tame-genus signature. These functions have prefix TG.
Examples:
TGIsIsomorphicTGSignatureTGPseudoIsometryGroup
More information
All the functions are documented in the TameGenus.pdf found at the repo.
P.A. Brooksbank, J. Maglione, J. B. Wilson
