Graded algebras are the path way between general algebraic structures and tensors. Suppose we have an algebriac structure $A$ and an index set $M$ which identifies a direct product decomposition
\[A=\bigoplus_{s:M}A_s.\]Often graded algebras arise from filters. You can see more about that in the filters package.
So the graded algebra assumption states that each $A_s$ is an abelian group and the following.
\[A_s*A_t \leq A_{s+t}.\]This sets up a number tensors, for example bilinear maps (3-tensors)
\[A_s\times A_t\rightarrowtail A_{s+t}\]but also tensors of general valence such as
\[A_{s_{\ell}}\times \cdots \times A_{s_1}\rightarrowtail A_{\sum_i s_i}.\]Graded algebra isomorphism.
In the graded algebra project we focus on isomorphism by searching out sections of $A$ that minimize the search. If these cannot be found we start a process of breaking up homogeneous components $A_s$ into smaller parts by refining the grading. Refinement is carried out by our filters package.
Here is an illustration of a bad layer, because its total surface area is larger.
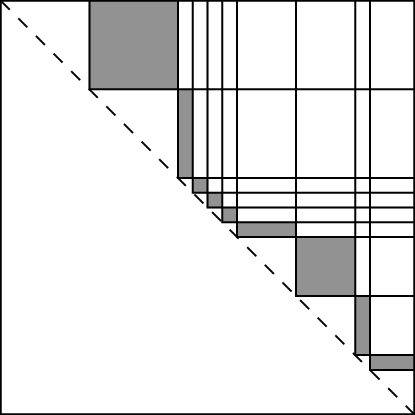
By refining and scanning the other layers we can find a potentially small surface area layer.
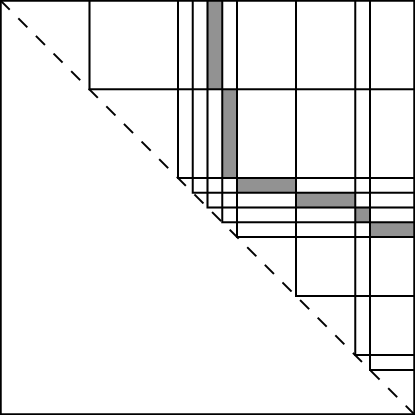
The ability to testing isomorphism from the middle is described in [BOW]. Further strategies for refinement were dealt with in [BGLQW].
References
-
[BOW] Isomorphism testing of Graded algebras, P.A. Brooksbank, E.A. O’Brien, J.B. Wilson, Trans. Amer. Math. Soc. 372 (11) 2019, 8067–8090. arXiv:1708.08873
-
[BGLQW] Incorporating Weisfeiler-Leman into algorithms for group isomorphism, Peter A. Brooksbank, Joshua A. Grochow, Yinan Li, Youming Qiao, James B. Wilson arXiv:1905.02518
P.A. Brooksbank, J. Maglione, J. B. Wilson
